Löysin Ylen areenan podcasteista vuonna 2015 tehdyn ’Tähtitieteen historian’, jossa toiseksi viimeisessä osassa Tapio Markkanen kertoi, että vuosina 1761 ja 1769 turkulainen Turun Akatemian professori Anders Planman mittasi tutkimusmatkoillaan Kajaanissa Venuksen Auringon ylikulun yhteydessä usean paikkakunnan maantieteellisen aseman.
Olin kyllä itsekin astrolabilla tehnyt auringon korkeuden mittausta, mutta korvat höröllä kuuntelin, että pituuspiirin mittauksessa hyödynnettiin Jupiterin Galilein kuiden kiertoa planeettan ympärillä. Tällä palstalla aiemmin mitattiin Galilein kuiden seuraamisella Jupiterin massaa, mutta minulle oli täysin uutta, että niistä saisi myös havaintopaikan pituuspiirin määritettyä.

Asia vaivasi minua pitkään, ja lopulta päätin selvittää, millä tavalla mittaukset todellisuudessa tehtiin. Otin avukseni matkaan Gemini 2.5 Pro tekoälyn, jonka kanssa mutkat suoristuivat, tosin monta kertaa jatkettiin väärällä tiellä. Olen kuitenkin hämmästynyt, miten tällä työkalulla saa niin merkittävällä tavalla laajennettua tietämystään. Itse olen kuitenkin vastuussa informaation paikkansapitävyydestä.
Planman teki 1762 Ruotsin kuninkaalliselle tiedeakatemialle artikkelin ”Kajaaninlinnan maantieteellinen asema”. Ja vuonna 1767 hän julkaisi artikkelin ”Astronomisia havaintoja matkalta Kajaaninlinnaan vuonna 1761” jossa raportoi 13 paikkakunnan leveyspiirin ja Kajaaninlinnan lisäksi viidelle näistä myös pituuspiirin.
Pitääkseni esityksen riittävän kompaktina, keskityn tässä artikkelissa leveyspiirin mittaamiseen. Pituuspiiristä ja Venuksen ylikulusta on tekeillä jatkoartikkelit kesän mittaan.
Planmanin tutkimuslaitteisto /1/
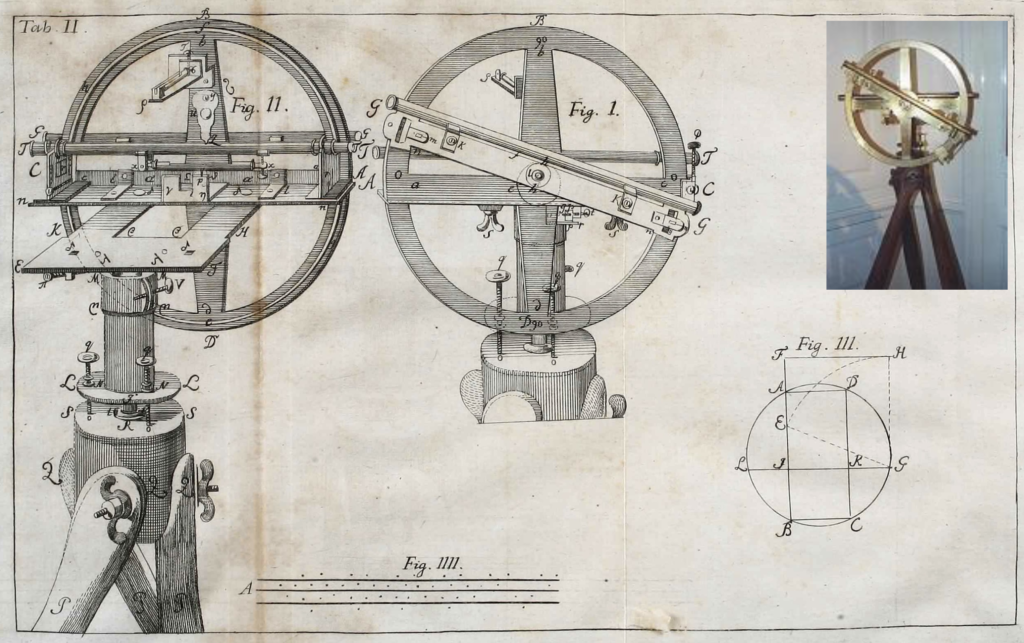
Tiedeakatemia oli varustanut Planmanin sen ajan huippulaitteistoilla. Maantieteellinen instrumentti oli vuonna 1750 suunniteltu alt-asimutaalinen teodoliitti, jolla mitattiin leveyspiirit. Laitteen esitteli Daniel Ekström Ruotsin kuninkaallisen tiedeakatemian julkaisussa ”Uusi maantieteellinen instrumentti”.
Instrumentissa on pieni kaukoputki sekä vaaka- että korkeuslukeman mittaamiseksi. Laitteessa on useampi vesivaaka, lukuisia säätöruuveja ja kolme liki metrin mittaista tukijalkaa.
Maantieteellistä paikannusta varten käytetään vain korkeusmittausta. Allaolevassa kuvassa näkyy keskellä korkeusmittauslevy, jonka päälle on asennettu 35 mm:n tähtäinputki, joissa on kaksi kuperaa ja säädettävää konveksilinssiä hiusristikon kera.
Levyn (G-G, leveys 45 mm, paksuus 0,4 mm) molemmissa päissä on pienet aukot, joiden yhteydessä on 19 viivaiset noniusasteikot. Liki puolen metrin halkaisijaisessa ympyrälevyssä on asteikot joka asteen kohdalla ja asteiden välissä on kolmasosa-asteen viivoitus. Näin sillä periaatteessa pääsee yhden kaariminuutin tarkkuuteen.
Planmanin mittauksista oli todennettavissa, että hän pystyi arvioimaan auringon korkeuden puolen kaariminuutin tarkkuudella.
Leveyspiirin määrittäminen auringon korkeudesta deklinaation avulla
Ennen Planmanin tuloksiin tutustumista, käydään läpi auringon korkeuden mittaamisen perusteet, jotka pätevät myös mm. sekstantilla mittaamiseen.
Johtuen maapallon 23,4 asteen kallistumasta kiertoradallaan aurinko on suoraan havainnoijan yläpuolella vuodenajasta riippuen kravun ja kauriin kääntöpiirien välillä. Vain kevät- ja syyspäivän tasauksen yhteydessä se on päiväntasaajalla eli se voidaan jättää huomioitta.
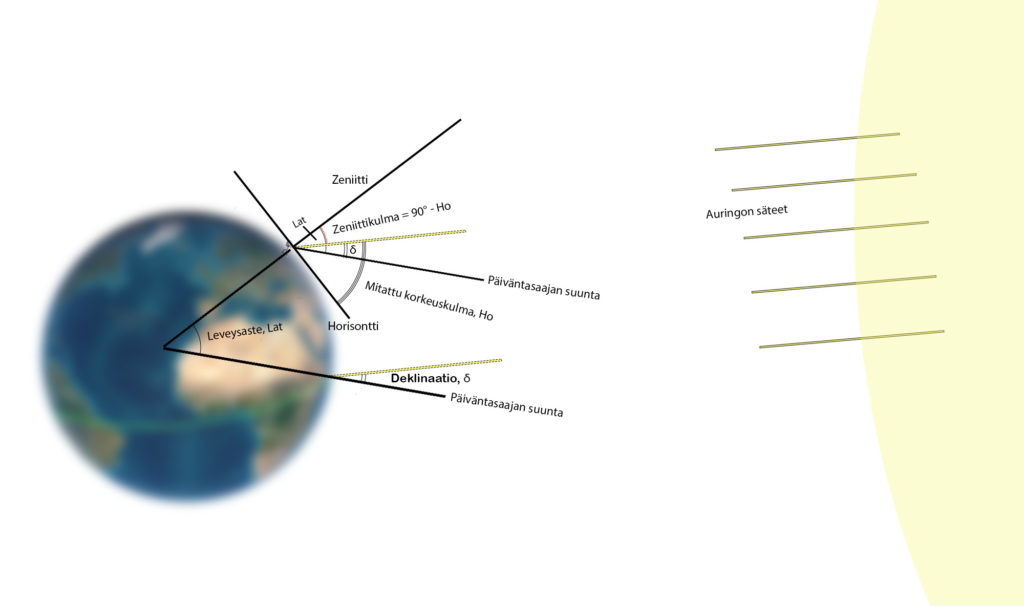
Auringon säteiden kulmaeroa ekvaattoriin kutsutaan deklinaatioksi, δ ja se on otettava huomioon leveyspiiriä määritettäessä. Kun aurinko on ekvaattorin pohjoispuolella deklinaatio on positiivinen ja eteläpuolella negatiivinen. Näinollen vain kevät- ja syyspäiväntasauksen aikaan deklinaatiota on nolla.
Deklinaation arvoja julkaistaan kalentereissa ja luotettavan lukeman saa myös yhdysvaltalaisen NOAA:n sivustolta.
Auringon leveyspiirin määrittelyssä käytetään auringon korkeuden komplementtikulmaa eli zeniittikulmaa Hz = 90° – Ho.
Kun mittaamme leveyspiiriä pohjoisella pallonpuoliskolla ja aurinko on etelässä päiväntasaajan yläpuolella, saamme leveyspiiriksi ylläolevan kuvan mukaisesti.
Lat = Hz + δ =(90° – Ho) + δ
Yhtälössä negatiivisen deklinaation yhteydessä leveyspiiri on korkeuslukemaa pienempi.
Auringon korkeuden määrittäminen
Vaikka instrumentilla onkin mitattu auringon korkeus, oikean tuloksen saaminen ei ole ihan sillä selvä. Käydään läpi tulokseemme vaikuttavat seikat.
- Korkeuslukema (Ha): Kulma, jonka luet suoraan laitteen asteikolta.
- Laitekalibrointi (Lk): Kalibroinnin jälkeen todettu laitteen oma pieni virhe, joka perustuu valmistajan tai käyttäjän tarkistukseen.
- Horisontin aleneminen (Hh): Korjaus, joka saattaa johtua mittalaitteissa, kuten sekstantin mittaustason sijainnista merenpinnan yläpuolella.
- Refraktio eli ilmakehän taittuminen (R): Ilmakehä taittaa valoa, jolloin taivaankappaleet näyttävät olevan korkeammalla kuin ne ovat.
- Parallaksi (P): Pieni korjaus, joka johtuu siitä, että mittaus tehdään Maan pinnalta eikä sen keskipisteestä.
- Auringon säde (Ar ): Korjaus, jos mittauspiste ei ole auringon keskellä.
1. Auringon korkeus, Ha
Auringon korkeus horisontista (Ha) muuttuu päivän mittaan, ja sen maksimikorkeus saavutetaan keskipäivällä. Tämä maksimikorkeus on riippuvainen leveysasteesta. Mitä pohjoisemmassa ollaan, sitä matalammalla Aurinko on taivaalla, ja mitä etelämpänä, sitä korkeammalla.
Leveyspiirit halkaisevat maapallon tasaisesti, ja kokonaisia asteita on 90 maapallon pohjoisella ja 90 maapallon eteläisellä pallonpuoliskolla. Aikoinaan huomattiin, että maapallon piiri on noin 40 000 km tai 21 600 meripeninkulmaa. Jaettuna 360:lla saadaan leveyspiireille yhden asteen arvoksi noin 60 meripeninkulmaa ja yhden kaariminuutin arvoksi yksi meripeninkulma. Vastaavasti yksi aste on noin 111 kilometriä ja yksi kaariminuutti 1 852 metriä.
Planman pystyi siis mittaamaan auringon korkeuden instrumentillaan puolen minuutin eli käytännössä hieman vajaan kilometrin tarkkuudella.
Auringon mittaaminen ei ole vaaratonta, urbaanilegendan mukaan moni kapteeni joutui käyttämään silmälappua loppuelämänsä pilatessaan silmänsä tässä yhteydessä. Siksi mittauksen yhteydessä on käytettävä suodatinta. Nykyään tiedämme, että aurinkoa voi katsoa vain auringonvalon liki 100% suodattamalla erikoissuotimella, mutta 1700-luvulla käytettiin erivärisiä linssejä. Uppsalasta raportoitiin vuonna 1761 /2/, että käytetyllä kaukoputkella saatiin auringon paiste kumottua punaisella suodinlasilla kun taas vihreällä suotimella auringonpilkut näkyivät huonommin. Toisella kaukoputkella taas päädyttiin käyttämään sekä punaista että vihreätä suodinta.
2. Laitekalibrointi, Lk
Mittalaitteen kalibrointia tehdään useammassa vaiheessa. Se voi olla valmistajan tekemä silloin, kun siihen käyttäjällä ei ole mahdollisuuksia sitä korjata. Joka tapauksessa käyttäjän vastuulla on tehdä perustarkistus ennen jokaista käyttöä. Sekstantilla tulee tehdä peilien suuntauksen tarkistus ja horisontin nollaus. Hyvin usein sitä ei saada täysin nollattua, vaan sekstantti antaa poikkeavan lähtölukeman. Korjaus voi olla negatiivinen tai positiivinen.
Planmanin instrumentissa oli oleellista varmistaa, että kaikki vesivaa’at olivat kohdallaan ja kaikki kiinnitykset paikallaan. Julkaisusta ei selviä, oliko valmistaja tehnyt laitteelle kalibrointeja, ja itselläni ei ole tietoa senaikaisista käytännöistä.
3. Horisontin aleneminen, Hh
Mikäli havainnoitsija sijaitsee horisonttia korkeammalla, on korkeuslukemasta vähennettävä kaariminuutteina
Hh = 1,76 * h0,5 (h = havaintopaikan korkeus h metreinä)
Itselleni tuli yllätyksenä, että havaintopaikan korkeudella (h) saattaa olla merkittävä vaikutus lopputulokseen. Esimerkiksi meren tai järven rannalla seisten h on noin kaksi metriä ja korjaus on jo huomattava eli noin 2,5 kaariminuuttia.
Planmanin käyttämä teodoliitti on tarkan leveyspiirin mittaamisessa aivan ylivoimainen. Koska sen toiminta perustuu tarkkaan vaakatasoon, ei tarvita sen enempää horisonttia kuin havaintopaikan korkeuden eron korjausta siihen.
4. – 6. Kokonaiskorjaus, Hkok
Taulukoissa usein kuten Nautical Almanc yhdistetään refraktio-, parallaksi- ja auringon sädekorjaukset yhdistetään kokonaiskorjaukseksi.
4. Taittovirheen korjaus
Auringon valo kulkiessaan ilmakehän läpi taittuu ja ilmiö korjataan refraktiokorjauksella, joka on aina negatiivinen. Se riippuu voimakkaasti havaitusta korkeudesta (Ha). Yksinkertainen ja melko tarkka kaava (korkeuksille yli 15 astetta) on kaariminuutteina
R = 1 / (tan(Ha))
Tangentin yhtälöstä johtuen korjaus on huomattava alle 15 asteen arvoilla ja silloin myös ilmakehän vaikutus lisää epävarmuutta.
5. Parallaksin kulmakorjaus
Havainnoitsijan ja maan keskipisteen kulmaerosta aurinkoon nähden tulee pieni positiivinen parallaksikorjaus. Korjaus on kaariminuutteina
P = 0,15 * cos(Ha)
Tyypillisesti parallaksikorjaus on noin 10% refraktiokorjauksesta
6. Mittauspisteen korjaus
Tarkkuutta vaatii myös mittauspisteen sijoittaminen. Keskelle aurinkoa sitä ei saa tarkasti, ja siksi suositaan joko auringon yläreunaa tai alareunaa. Vielä edelleen esimerkiksi sekstantin käyttäjiä suositellaan valitsemaan horisontti ja auringon ala- tai yläreuna mittaustavaksi. Mutta sitten on huomioitava, että mittauksessa saadaan tulokseksi joko positiivinen auringon sädekorjaus (yläreuna) tai negatiivinen auringon sädekorjaus (alareuna).
Auringon halkaisija on meille tuttu puoli astetta eli säde on 15 kaariminuuttia. Sen pois jättäminen siis aiheuttaisi todella ison virheen eli liki 30 kilometriä. Mutta … maapallomme ei kierrä ympyrärataa vaan hieman elliptistä ja meiltä katsottuna auringon säde (Ar) vaihtelee 15.8 kaariminuutin (heinäkuu) ja 16.3 kaariminuutin (tammikuu) välillä. Hiusten halkomista ehkä, mutta enimmillään puolen kaariminuutin ero aiheuttaa vajaan kilometrin virheen.
Kun tuon periaatteen tietää, voi korjauksen arvioida suurin piirtein, mutta tuloksen saa myös kaariminuuttina yhtälöllä
Ar = 16,05 * (1−0,01672∗cos(0,9856∗(päivä−4)))
Yhtälössä päivä on juokseva päivän lukema vuoden alusta laskien. Käytännössä tähtitieteilijät käyttivät valmiita taulukoita, mutta tämä yhtälö näyttää, miten arvo periaatteessa lasketaan.
Edelliset kolme korjausta yhdistettynä on haluttu kokonaiskorjaus
Hkok = – R + P +/- Ar
Jos laskemisen sijasta haluaa käyttää taulukkoa, niissä kokonaiskorjaus annetaan erikseen auringon ylä- ja alareunalle..
Yhteenveto korkeuden mittaamisesta
Näinollen todellinen auringon korkeus horisontista on
Ho = Ha +/- Lk – Hh + Hkok
Minusta on tärkeätä oivaltaa, että oikean korkeuden miittamiseksi itse mittalaitteen tarkkuuteen ei saa keskittää huomiotaan, sillä mittausolosuhteiden määrittelyssä helposti tehdään moninkertainen virhe.
Planmanin mittaustulokset
Planman julkaisi Ruotsin kuninkaallisen akatemian julkaisussa erikseen Kajaaninlinnan ja Oulun leveyspiirimittauksensa tulokset. Olisin mielelläni yrittänyt verifioida tuloksia tarkemmin, mutta julkaisuissa ei ollut kaikkia käytettyjä edellämainittuja korjauksia. Deklinaatiokorjaus on hänen teksteissä oletettu itsestäänselväksi enkä ole löytänyt edes mainitaan käytetystä taulukosta. Lisäksi ajoittain on mainittu sekä refraktio- että parallaksikorjausten tekemistä, mutta niissä on viitattu senaikaisiin taulukoihin ilman tarkempaa viitettä. Hän ei tarvinnut mittauspaikan korkeuskorjausta, koska korkeusmittauslaite oli vaaitettu vaakatasoon.
Kajaaninlinnan leveyspiiri /3/
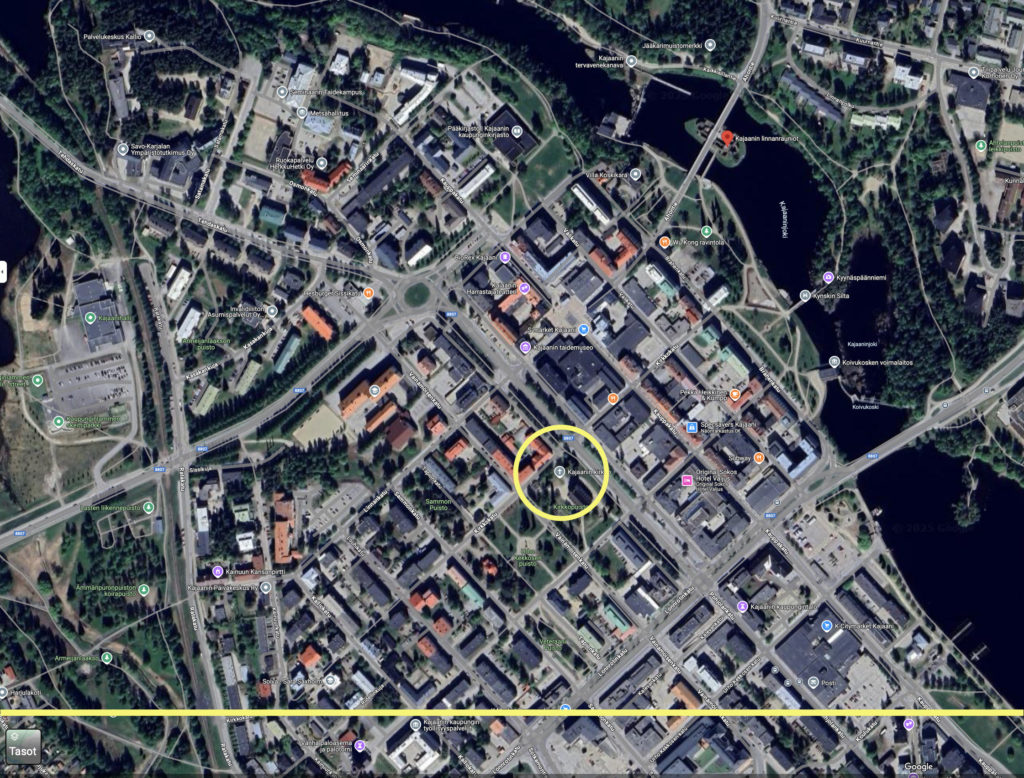
Korjaus 23.7.2023 – Koska Planman puhui Kajaaninlinnasta, oletin sen tarkoittavan itse linnaa. Mutta linnahan on tuhoutunut muutama vuosikymmen ja kun tarkemmin katsoin, mittausvälineet sijoitettin kellotapuliin eli kirkon luo. Kajaanin kolme kirkkoa ovat olleet samalla paikalla, joten uuden tarkastuksen jälkeen Planmanin sihti oli vieläkin tarkempi
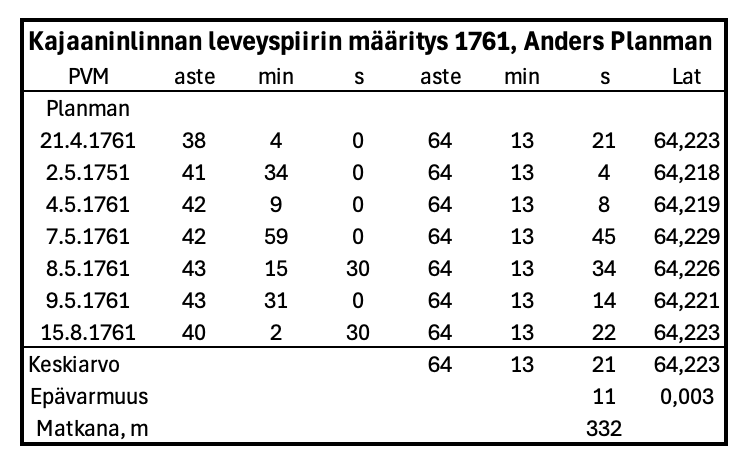
Mittauksia on tehty seitsemän kappaletta aikavälillä huhtikuun loppu ja elokuun puoliväli. Koska mittauksia on seitsemän kappaletta, Planmanin tuloksesta tulee tarkempi. Keskihajonnan avulla saadaan 95% epävarmuudella tulokseksi +/- 11 kaarisekuntia, joka on matkana +/- 332 metriä.
Kajaaninlinnan tarkka nykyinen leveyspiiri on 64° 13′ 45”, joten siihen nähden ollaan 24 kaarisekuntia tai 740 metriä etelässä. Tosin Planman on pyörittänyt keskiarvon puolen minuutin tarkkuudelle, ja tässä tapauksessa pyöristys pienentää eroa kahdeksan kaarisekunnin verran, kun hän ilmoittaa Kajaaninlinnan leveyspiiriksi 64° 13′ 30”.
Planman pyöristystä puoltavana seikkana oli myös hänen toukokuussa kahtena yönä mittaamansa Arcturuksen yläkulminaation korkeus 46° 14′, josta sai Kajaanin leveyspiiriksi 64° 13′ 30”. Tämän mittauksen itsekin pystyin vahvistamaan Stellariumin avulla oikean suuntaiseksi.
Planman oli tarkistanut mittausinstrumenttinsa hyvin säntillisesti eikä niissä esiintynyt muutostarpeita. Lisäksi laitteistoa oli säilytetty erittäin turvallisesti. Planman mainitsee julkaisussaan, että vuonna 1758 tehty leveyspiirin edellinen lukema oli ollut 16 kaariminuuttia eli noin 30 kilometriä liian suuri. Mittaus oli tehty Euroopan Karttaa varten ranskalaisten toimesta.
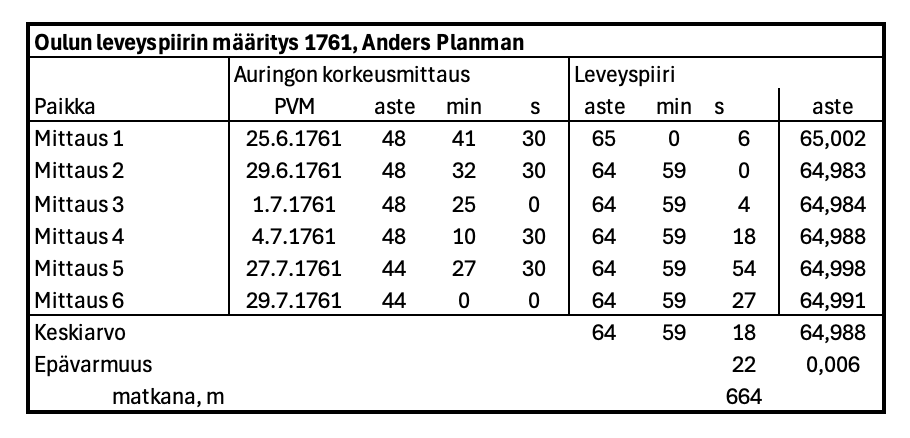
Oulun leveyspiiri /4/
Oulun leveyspiirin Planman mittasi kuusi kertaa noin yhden kuukauden aikana. Mittausten hajonta oli kaksinkertainen Kajaaninlinnaan verrattuna, epävarmuus on +/- 22 kaarisekuntia, joka matkana vastaa +/- 664 metriä.
Julkaisusta ei ilmennyt tarkkaa paikkaa eikä ole täysin selvää, missä Planmanin mittaukset tehtiin. Koska laitteiston siirtämistä varmasti välteltiin, käytän oletusarvona käytän Oulun vanhaa pappilaa, joka sijaitsee Asemakadulla leveyspiirillä 65° 0′ 49”. Mikäli hän teki mittauksensa pappilasta, on Planmanin ilmoittama sijainti 1,5 kaariminuuttia eli noin 2,8 kilometriä etelämpänä.
Tämän julkaisun suhteen on mielenkiintoista, että Planman julkaisi sen vasta vuonna 1767 eli kuusi vuotta mittauksia myöhemmin. Ehkäpä hän sen myötä valmisteli tulevaa vuoden 1769 Venuksen ylikulun tallentamista.
Muut paikkakunnat
Kajaaninlinnassa tehtyjen mittausten lisäksi huhtikuun 1761 ja tammikuun 1762 välisenä aikana Planman tiedeakatemian pyytämiä Suomen paikkakuntien koordinaatteja. Hän mittasi 11 muun paikkakunnan leveyspiirit oheisen taulukon mukaan, johon olen liittänyt myös vertailun Google Mapsin dataan. Artikkelissaan 1767 hän jostain syystä jätti mainitsematta usean paikkakunnan auringon korkeuden, vaan raportoi ainoastaan leveyspiirin.
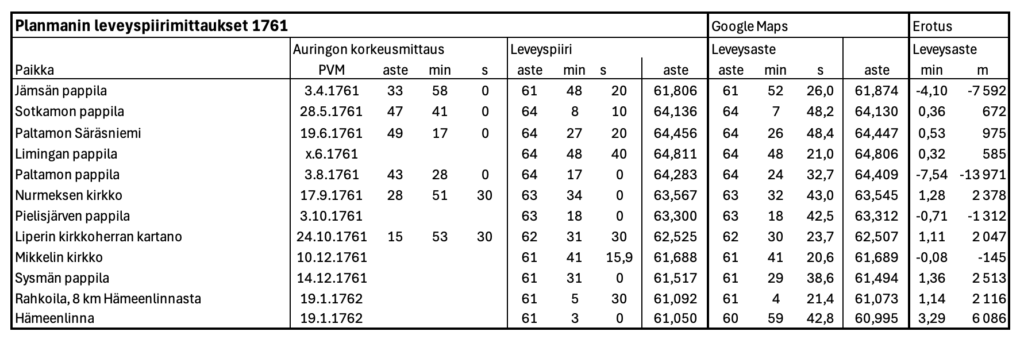
Mittaustuloksista näkyy selvästi, miten leveysasteen mittauksissa mittausten lukumäärä merkittävästi vaikuttaa tulokseen. Planman ei mainitse, tekikö hän useampia mittauksia, mutta tulokset ovat kaikki heikompia kuin Kajaaninlinnassa tai Oulussa. Lisäksi virhettä voi aiheuttaa se, että on vaikea varmistaa tarkka mittauspaikka.
Kolmella paikkakunnalla ero on alle kilometrin, neljällä alle kolme kilometriä, kolmella 6 – 8 kilometriä ja yhden paikkakunnan tarkkuus eroaa melkein 14 kilometriä.
Yhteenveto
Vaikka Planmanin mittauksissa leveyspiirin erot näkyvät kuvissa ehkä merkittävinä, ovat tulokset todella tarkkoja. Mittausten epävarmuus on pienempi kuin mittauslaitteiston pienin jakoväli. Vaikka absoluuttinen virhe nykypäivän arvoihin on suurempi, sen selvittäminen ei välttämättä 260 vuoden takaa ole helppoa.
Planman raportoi Ruotsiin ruotsiksi, mutta väitöskirjansa ja muita raportteja kirjoitettiin latinaksi, joka oli 1700-luvulla kansainvälinen tiedekieli.
Minusta on ollut häkellyttävän mielenkiintoista lukea 1700-luvun tiedejulkaisuja. Olen ollut yllättynyt mittausten tarkkuudesta ja tutkijoiden pieteetistä saada mahdollisimman tarkka tulos.
(Muut paikkakunnat lisätty 19.7.2025)
Lähteet
[1] Ekström, Daniel. Et Nyt Geografisk Instrument, Kungliga Svenska Vetenskapsakademiens Handlingar, Januari, Februari och Mars i år 1750, pp. 26 – 44.
[2] Wargentin, Pehr (ed.). OBSERVATIONER På Planeten Veneris gång genom Solens Discus, om äro gjorde i Stockholm, Upsala, Åbo, Carlscrona, Lund, Landscrona, Cajaneborg den 6 Junii 1761. Kungliga Svenska Vetenskapsakademiens Handlingar, April, Maj och Juni i år 1761, pp. 143 – 166.
[3] Planman, Anders. Cajaneborgs geografiska belägenhet, Kungliga Svenska Vetenskapsakademiens Handlingar, April, Maj och Juni i år 1762, pp. 132 – 139.
[4] Planman, Anders. Astronomiska observationer under resan til och ifrån Cajaneborg, gjorde år 1761. Kungliga Svenska Vetenskapsakademiens Handlingar, Januari, Februari och Mars i år 1767, pp. 132 – 139.
