Löysin Ylen areenan podcasteista vuonna 2015 tehdyn ’Tähtitieteen historian’, jonka toiseksi viimeisessä osassa Tapio Markkanen kertoi, että vuosina 1761 ja 1769 turkulainen Turun Akatemian professori Anders Planman mittasi Venuksen ylikulun havaintomatkoillaan Suomessa usean paikkakunnan maantieteellisen aseman.
Paikkakunnan leveyspiirin mittaamisesta 260 vuotta sitten on aiempi artikkeli ja nyt tutustutaan silloiseen tapaan mitata pituuspiiri. Kesän mittaan on tarkoitus vielä lisätä artikkeli Venuksen ylikuluista 1760-luvulla.
Paikkakunnan pituuspiirin mittaamiselle 1760-luvulla suurin haaste oli saada paikallinen kellonaika tarkasti selville. Meriliikenteessä ajan epävarmuus aiheutti vuosittain paljon laivojen ja ihmishenkien menetyksiä eikä se ollut yksinkertaista maan kamarallakaan.
Pituuspiirin määrittäminen
Pituuspiiri kulkee navalta toiselle ja Yhdistyneen kuningaskunnan Greenwichissä kautta kulkee pituuspiiri 0 eli nollameridiaani.
Pituuspiirit kohtaavat navoilla, minkä vuoksi niiden välinen etäisyys pienenee päiväntasaajalta siirryttäessä. Vain päiväntasaajalla yhden asteen ero pituuspiirien välillä vastaa 60 meripeninkulmaa (noin 111 km).
Maan pyörimisen vuoksi Aurinko näyttää liikkuvan taivaalla 15 astetta tunnissa. Tämä yhteys pituusasteiden ja ajan välillä on aikavyöhykkeiden perusta. Tästä syystä 1700-luvulla yhtenäisen nollameridiaanin puuttuessa, kerrottiin uuden paikkakunnan pituuspiiri aikaerona tunnettuun paikkakuntaan.
Kun siirrytään pohjoiseen tai etelään, pituuspiirien välinen yhden asteen matka ei enää tarkoita 60 merimailia. Suomessa Helsingin kohdalla asteen ero pituuspiirien välillä vastaa 30 meripeninkulman matkaa. Laskennallisesti etäisyys kahden pituuspiirin välillä tietyllä leveysasteella saadaan kertomalla päiväntasaajan etäisyys (60 meripeninkulmaa) kyseisen leveysasteen kosinilla.
Pituuspiirin määrittämiseen tarvitaan havainto tunnetusta taivaan tapahtumasta ja hyvin tarkka kello. Jo minuutin heitto aiheuttaa enimmillään meripeninkulman virheen. Planman käytti useita eri havaintotapoja ja hänellä oli hyvin tarkka kello, josta pidettiin erittäin hyvää huolta.
Kellon tarkistus /1/
Tutkimusmatkoillaan 1761 ja 1769 Planmanilla oli ”astronominen kello, jonka on valmistanut erinomainen taitaja ERNST Tukholmassa ja joka on varustettu heilurilla, joka on koottu messinki- ja rautatangoista”. Heilurimaininta viittaa useista rinnakkaisista messinki- ja rautatangoista koostuneeseen kompensaatioheiluriin (gridiron pendulum), joka oli aikansa ehdotonta huipputeknologiaa. John Harrison oli kehittänyt tekniikan neljä vuosikymmentä aiemmin vähentääkseen lämpötilan muutosten vaikutusta heilurin pituuteen, mikä teki kellosta erittäin tarkan.
”Nämä instrumentit siirrettiin toukokuun 30. päivänä kellotapuliin, josta avautui vapaampi näkymä Auringon nousuun ja laskuun. Kello sijoitettiin tämän rakennuksen alaosaan, mahdollisimman vakaaseen ja lujaan paikkaan, ja lisäksi niin vahvoilla lukoilla suojattuna, ettei kenelläkään ollut sinne pääsyä JOHTAJAN tietämättä. Eikä pienintäkään epäilystä rakennuksen tärähtelystä syntyisi, oli huolehdittu siitä, että Auringon päivänä merkkiä ei annettu temppeliin, ellei kellotapulin kelloa soitettu kevyesti kolme tai neljä kertaa.”
Nämä varotoimet vakaan paikan, lukitusten ja kellojen soiton rajoitusten suhteen kertovat äärimmäisestä huolellisuudesta.
Mittaustulokset
Heilurikellon tarkistuslaskelmat olivat ilahduttava näky, koska niissä olivat kaikki olennaiset asiat esillä. Näillä Planman kiistatta osoittaa paikallisen keskipäivän olevan tarkan. Laskelmissa esiintyy myös harvinainen terssi (”’), joka on sekunnin 1/60 osa.

Tämä 255 vuotta vanha taulukko on elegantti esitys siitä, miten 1700-luvun tähtitieteilijä käytti yksinkertaista geometriaa ja huolellista toistoa saavuttaakseen hämmästyttävän tarkkuuden paikallisajan määrityksessä. Se on raakadataa, joka todistaa hänen työnsä laadun.
Tarkempaa tarkastelua varten esitetään myös suomennettuna koko laskentataulukko. Koska kello tarkistetaan keskipäivän auringon avulla, se ei onnistu pilvisenä päivänä. Tämän takia Planman oli varautunut tilanteeseen ja teki päivittäin tarkistuksia. Hänellä oli melko suotuisat olosuhteet, sillä ainoastaan Venuksen ylikulun päivänä ei keskipäivän aikaa saatu mitattua.
Kuitenkin mittaustulokset 2.6., 4.6. ja 5.6. pelastivat tilanteen. Taulukon 3.6. päivän rivistö on harmaataustainen, sillä se perustuu muiden päivien mittauksesta laskemiini interpolointeihin.
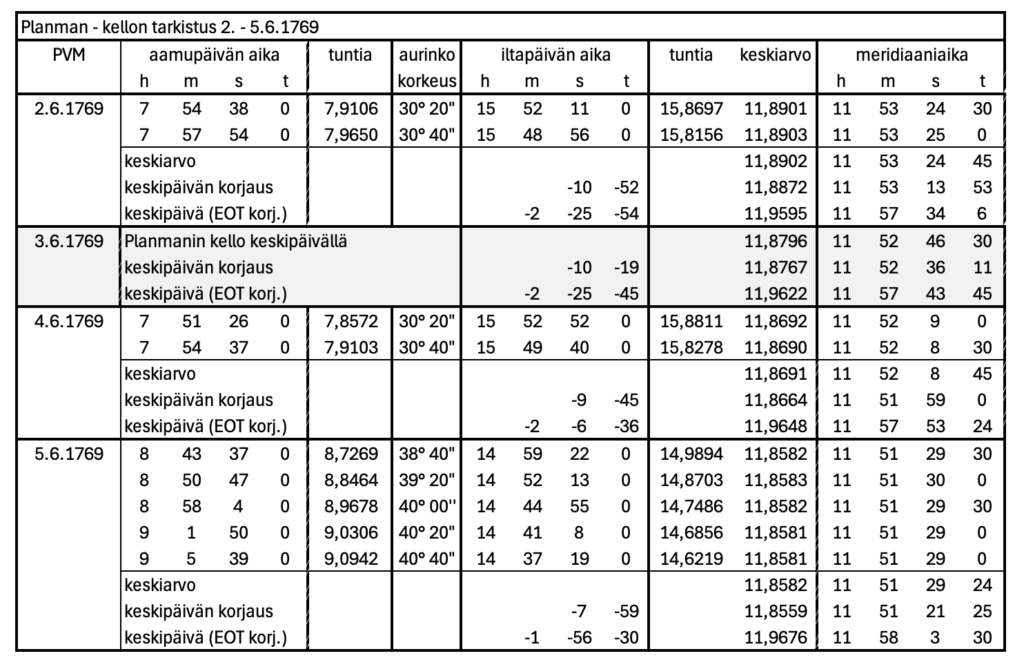
Koska auringon korkeus meridiaaniohituksen yhteydessä muuttuu hyvin vähän, on tarkan keskipäivän hetken mittaus tehty monta tunti ennen ja jälkeen samalla auringon korkeudella, kuvan tapauksessa korkeuksilla 33° 20′ ja 33° 40′. Kummankin korkeuden ajoista on laskettu keskiarvo, joista huomataan 2.6. vain 0,5 sekunnin ero kahden korkeuden välillä. Koska heilurikello antoi ajan vain sekunnin tarkkuudella, tuloksen heitto on pienin mahdollinen.
Käytetty keskiarvo ei kuitenkaan ollut Planmanille riittävän tarkka, sillä 1769 tiedettiin, ettei auringon kaari taivaalla ole täydellisen symmetrinen keskipäivän molemmin puolin vaan auringon deklinaatio taivaalla on jatkuvassa liikkeessä maapallon radalla auringon ympäri. Siksi Planman suorittaa kaikkien päivien kohdalle keskipäivän korjauksen. Kesäkuun alussa lähellä kesäpäiväntasausta auringon liike taivaalla on iltapäivällä aavistuksen nopeampi ja siksi keskipäivä on hieman keskiarvoa aiemmin. Koska kesäpäiväntasaus, jolloin deklinaation suunta muuttuu, on lähellä, on korjaus vain muutamia sekunteja. Ja taulukosta huomaamme, että tämä keskipäivän korjaus pienenee päivien edetessä. Lopputuloksena on kunakin päivänä heilurikellon mittaama keskipäivä.
Maapallon kiertorata aiheutta myös tarpeen ajantasaukselle (EOT, Equation of Time). Kesäkuun alussa se on muutamia minuutteja negatiivinen lähestyen nollaa kesäpäiväntasauksessa. Ajantasauksen aika vähennetää keskipäivän hetkestä 12:00:00 ja saadaan paikallinen keskipäivä.
Tämän jälkeen Planman laski kullekin päivälle kellon ja paikallisen keskipäivän erotuksen
- 2.6. 1761 erotus on 4 minuuttia 20 sekuntia ja 13 terssiä
- 4.6. 1761 erotus on 5 minuuttia 54 sekuntia ja 24 terssiä
- 5.6. 1761 erotus on 6 minuuttia 42 sekuntia ja 5 terssiä
Olennaista on, että vaikka kellon ilmoittama aika ei pysynyt kohdallaan, Planman mittauksilla osoitti, että sen sen heilurikoneisto onnistui pitämään kellon hidastumisen keston vakaana, ollen 47 sekuntia 21 terssiä +/- 36 terssiä. Tämän perusteella laskien saadaan, että kesäkuun 3. päivän todellinen keskipäivä kellon mukaan oli puolen sekunnin tarkkuudella 11h 52′ 36.”16”’.
Planmanin julkaisun taulukko ja jatkolaskelmat osoittavat, miten 1700-luvun tähtitieteilijä käytti yksinkertaista geometriaa ja huolellista toistoa saavuttaakseen näin hämmästyttävän tarkkuuden paikallisajan määrityksessä. Tämä raakadata todistaa hänen työnsä laadun.
Planmanin kaukoputket
Havainnointiretkien kaukoputkien koot oli aivan hirmuisia tämän päivän harrastajien silmissä. Matkassa oli mukana kolme kaukoputkea, tosin akromaattinen putki vaihtui toiseen vuonna 1769.
- Venuksen ylikulkua varten oli astronominen kaukoputki, jonka polttoväli oli 21 Ruotsin jalkaa eli 6235 mm ja okulaarin 2,9 Ruotsin tuumaa eli 72 mm. Tällöin kaukoputken suurennus on 87-kertainen. Voi vain kuvitella, mitä hankaluuksia on ollut sekä kuljetuksessa että käytössä. Pitkä polttoväli oli keino vähentää 1700-luvun alun kaukoputkia vaivannutta kromaattista vääristymää valon värien kohdistuessa eri polttopisteisiin.
- Planeettoja ja tähtimittausta varten astronominen kaukoputki, jonka polttoväli oli kuusi jalkaa eli 1782 mm. Kaukoputki on varustettuna mikrometrillä, säädettävällä hiusristikolla.
- Uudenaikaisimpia olivat akromaattiset kaukoputket. Vuonna 1761 retkikunta sai mukaansa uuden, John Dollondin valmistaman kaksoislinssikaukoputken, jolla ’lyhyempi’ putki väisti värivirheet. Kaukoputken polttoväli oli 5,5 jalkaa eli 1633 mm ja se oli valmistettu vuoden 1758 jälkeen. Vuonna 1769 kaukoputki vaihtui pienempään ja sen polttoväli oli 3 jalkaa eli 891 mm ja okulaarin 22,3 mm. Tällöin kaukoputki suurentaa kohteiden halkaisijaa 40-kertaisesti.

Planmanin pituuspiirimittaukset
Koska Venuksen ylikulut tapahtuivat 1761 ja 1769, Anders Planman teki kaksi havaintomatkaa. Vuonna 1761 oli tarkoitus mennä Lappiin asti, mutta talvi oli ollut runsasluminen ja hän valitsi Kajaanin havaintopaikakseen. Ilmeisesti olosuhteet olivat olleet niin tyydyttävät, että myös 1769 matka suuntautui Kajaaniin.
Kajaaninlinnan pituuspiiri 1761 /2/
Planman oli saapunut Kajaanin hyvissä ajoin ennen Venuksen ylikulkua, sillä päänäytöstä ennen olisi sekä kuun- että auringonpimennykset, joista hän teki ensimmäiset leveyspiirin mittaukset Myöhemmin syksyllä palattuaan Suomen kiertomatkaltaan takaisin Kajaaniin, hän myös mittasi leveyspiirin Jupiterin kuiden avulla.
Menetelmä 1: Kuunpimennys 18. toukokuuta 1761
Kuunpimennyksessä maan varjo liikkuu Kuun pinnalla. Pimennys näkyy maapallolla kaikille havaitsijoille täsmälleen samalla hetkellä. Verrattaessa kellonaikoja, jolloin tietyt Kuun kraatterit (esim. Grimaldus, Aristarchus, Mare Crisium) pimenevät tai ilmestyvät varjosta Kajaanissa ja Tukholmassa, saadaan selville näiden paikkakuntien välinen aikaero ja sitä myötä pituuspiiriero.
Pimentymisvaiheessa Planman seurasi yksityiskohtaisesti kuun kraaterien peittymistä. Hän käytti mikrometrillä varustettua linssikaukoputkea ja keräsi 26 havaintoa kuunpimennyksen aikana. Kun katson tuota listaa, joka kerättiin 80 minuutin aikana, lisää se omalta osaltaan kunnioitustani tuon ajan ammattilaisen tekemiseen.
Täyspimennyksen aikana pilvet tulivat tielle, eikä Planman pystynyt näkemään kuun kirkastumista, mutta sai kuitenkin kaksi havaintoa kohta kirkastumisen alettua. Sitten tuli tunnin tauko ja viimeisen neljän minuutin aikana rekisteröitiin kaksi havaintoa.
Hän vertasi 25 selkeimmän havainnon keskimääräistä eroa Tukholman observatoriossa tehtyihin vastaaviin havaintoihin ja sai tulokseksi, että Kajaaninlinna on 38 minuuttia ja 40 sekuntia Tukholman observatoriosta itään.
Menetelmä 2: Auringonpimennys, 3. kesäkuuta 1761
Auringonpimennyksen vertailu on monimutkaisempi tapa mitata leveyspiiri, sillä auringon 150 miljoonan kilometrin etäisyyden vuoksi täyspimennys tekee vaelluksen maapallon pinnalla. Yleensä pimennyksen loppumishetki on parhaiten kellotettavissa.
Kajaanin korkeudella nähtiin 5/6 auringonpimennys ja Planman rekisteröi pimennyksen loppumishetken Kajaaninlinnassa. Hän vertasi tätä tulosta Torniossa Anders Hellantin tekemään havaintoon. Huomioituaan paikkakuntien välisen parallaksin, hän sai aikaeron Kajaanin ja Tornion väliseksi aikaeroksi tasan 14 minuuttia. Tornion ja Tukholman välinen aikaeron tiedettiin olevan 24 minuuttia 38 sekuntia ja siten Kajaaninlinnan ja Tukholman väliseksi aikaeroksi tulee tällä menetelmällä 38 minuuttia 38 sekuntia.
Tulos vastaa hyvin kuunpimennyksen tuloksia, tosin tarkempi analyysi osoittaa, että Tornion pituuspiiri oli 20 sekuntia lännempänä. Asia huomattiin 1769, jolloin Uppsalan tähtitieteilijä Fredric Mallet tarkasti Hellantin mittaukset /3/. Tämä korjaus aiheuttaa lisävirhettä 20 sekuntia, joten Torniossa tehdyssä auringonpimennyksen arvioinnissa ei oltu myöskään täysin täysin onnistuttu.
Menetelmä 3: Jupiterin kuiden pimennykset syyskuu 1761
Galileo Galilei oli 1600-luvun alkupuolella esittänyt, että Jupiterin kuiden säännölliset katoamiset ja ilmestymiset planeetan varjosta ovat universaaleja aika-merkkejä. Ja näin antavat mahdollisuuden ajan tarkistamiseen.
Menetelmää ajan tarkistamiseksi kaivattiin erityisesti merenkulussa, jossa laivoja säännöllisesti menetettiin, mutta menetelmää ei saatu sopivaksi keinuvilla laivoilla. Meni 150 vuotta, ennenkuin riittävän tarkka laivakronometri ratkaisi ongelman.
Kuitenkin maalla tällä menetelmällä saavutettiin kohtalainen tarkkuus ja se oli kolmionmittausta huomattavasti nopeampi menetelmä jopa senaikaisilla kaukoputkilla ja kelloilla. Planman teki pituuspiirin tarkistusmittauksia kahdesti syyskuussa 1761.
3.9. 1761 Planman havaitsi Ganymedeksen katoamisen Jupiterin varjoon 21 jalan kaukoputkella. Hän vertasi aikaansa Anders Hellantin Torniossa vastaavalla kaukoputkella tekemään havaintoon ja sai tulokseksi Kajaanin ja Tornion väliseksi aikaeroksi 14 minuuttia 19 sekuntia, mikä itse asiassa heittää vain kaksi sekuntia oikeasta lukemasta. Hellant oli siis onnistunut mittauksissaan tällä kertaa. Mutta kun Planman lisäsi arvoon Tornion ja Tukholman virheellisen etäisyyden, tuli Kajaaninlinnan etäisyydeksi Tukholmasta 38 min 57 sekuntia.
8.9 1761 Planman havaitsi Io:n pimennyksen. Hän vertasi tätä aikaa Marseillessa tehtyyn havaintoon ja sai aikaeroksi 1 tunti 28 minuuttia 35 sekuntia. Marseillen ja Tukholman etäisyys tiedettiin olevan 37 minuuttia 54 sekuntia, joten välille Kajaaninlinna – Tukholma jäi 37 minuuttia 54 sekuntia. Mittauksen suhteen Planman ei ollut tyytyväinen, sillä Io oli ollut lähellä horisonttia kun taas Marseillessa Io oli ollut korkeammalla kirkkaammin näkyvissä.
Näistä kahdesta mittauksesta Planman sai keskiarvoksi 38 minuuttia 26 sekuntia.
Pieni välipala
Ennen kuin liian tiukasti arvostellaan tähtitieteen harrastajan Hellantin toimintaa, laitan tähän animaation, miltä tuo 3.9. havainto näytti. Voit itse arvella, miten tarkkaan ilmiön voi kellottaa. Animaatio on tehty Stellariumin avulla, ja sen noin 50 minuuttia on nopeutettu 25 sekuntiin.
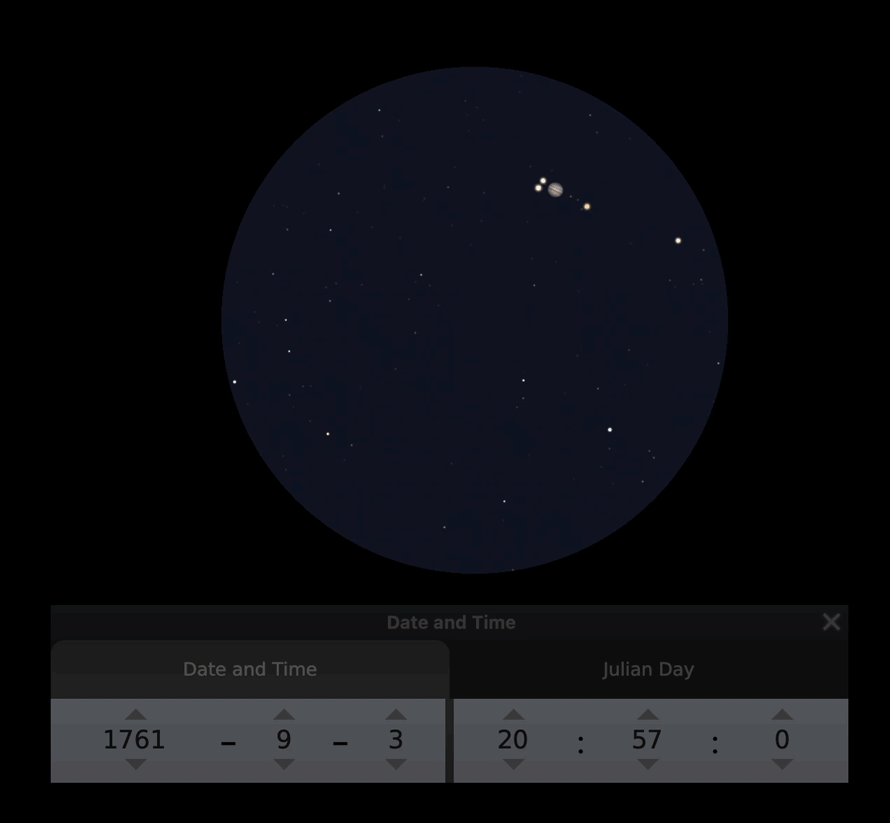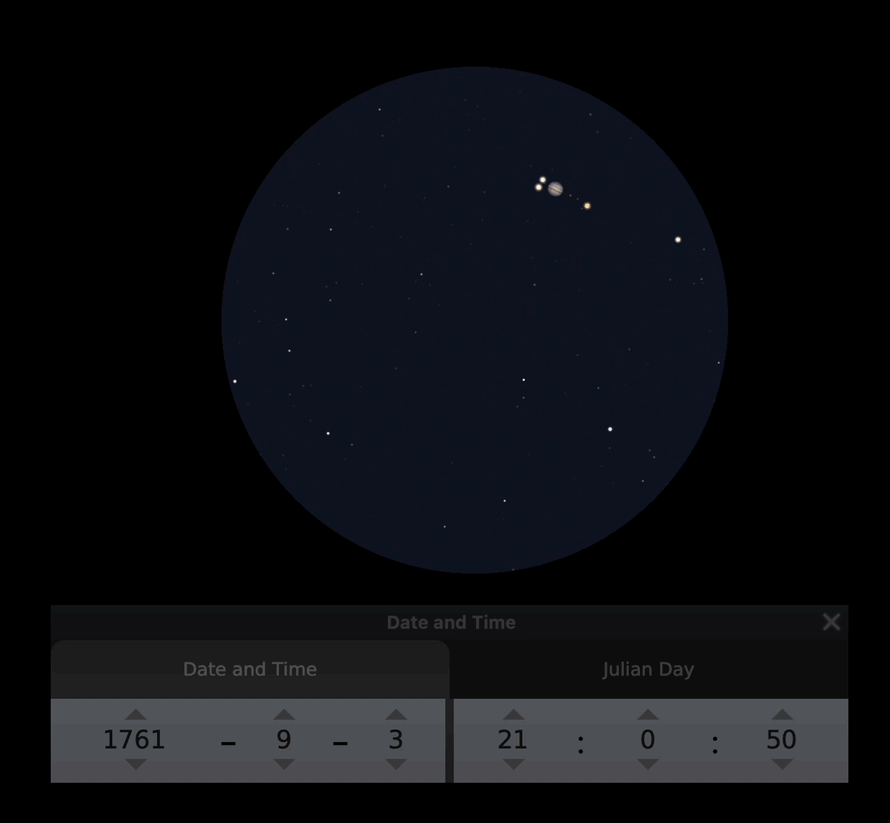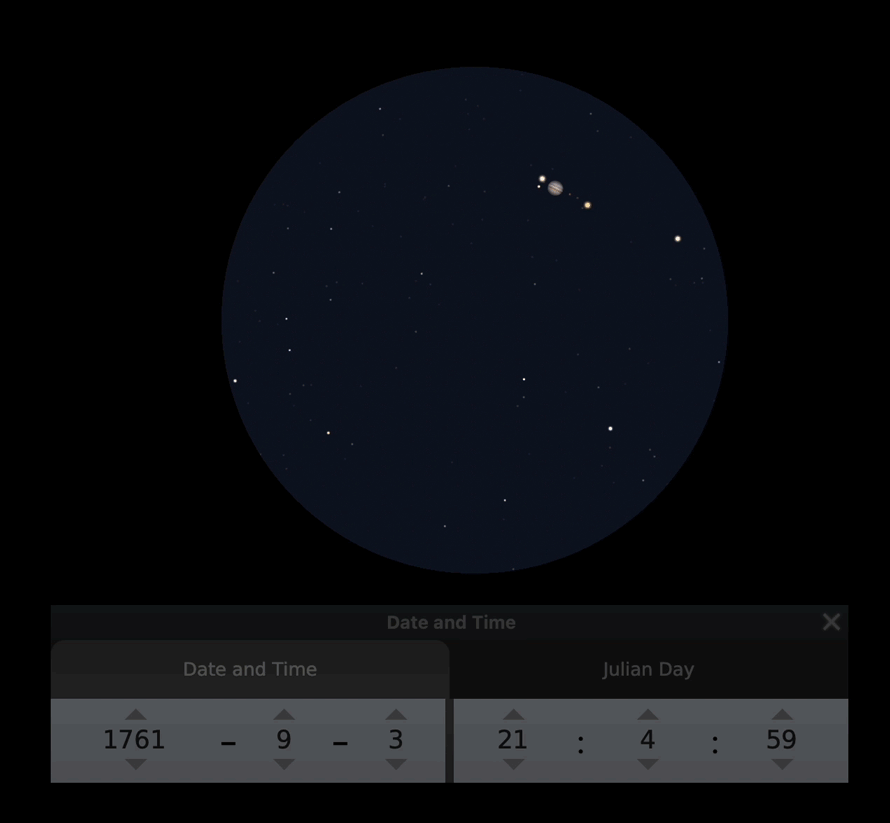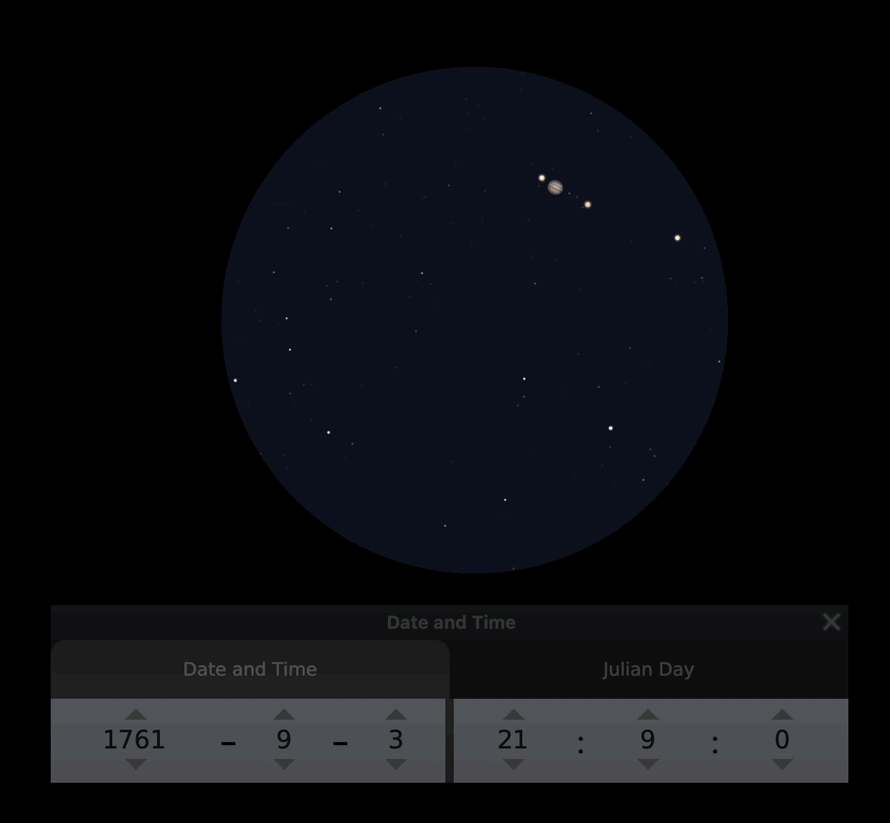
Yhteenveto Kajaaninlinnan mittauksista
Planman oli saanut hieman ristiriitaisia tuloksia, mutta hän suoriutui erinomaisesti, kun mittauksia arvioidaan näin jälkeenpäin. Huolellinen mittaus ja hyvä laitteisto mahdollisti tarkan mittaamisen.
Punnittuaan mittaustuloksia (sanaleikki suotakoon) Planman painotti Kuunpimennyksen lukuisia mittauksia ja ilmoitti Kajaaninlinnan etäisyydeksi Tukholman observatorioon olevan 38 minuuttia 40 sekuntia. Ja tämä lukema Google Mapsin mukaan heittää kelloetäisyytenä vain kaksi sekuntia!


Hän myös mainitsee artikkelissaan, että Kajaaninlinnan aiemmat mittaukset olivat liikaa idässä, vuonna 1747 mitattu pituuspiiri 25 minuuttia (20 km, Ruotsin kartassa) ja vuonna 1758 mitattu pituuspiiri 8 minuuttia (6,5 km, Euroopan kartassa).
Mielenkiintoinen yksityiskohta on, että tiedeakatemian tuoreeltaan julkaisemassa yhteenvedossa Ruotsin tekemistä Venuksen ylikulun tuloksista kerrotaan kyllä Anders Planmanin 18.5.1761 tekemästä pituuspiirin mittauksesta, mutta tulokseksi kerrotaan ”noin 39 minuuttia 20 sekuntia” /4/.
Planman korjasi yhden aikavirheen Venuksen ylikulun kohdalla vuotta myöhemmin julkaistussa artikkelissaan Kajaaninlinnan maantietellisestä asemasta. Mutta hän ei puutu yllämainittuun pituuspiirin arvoon, vaikka yksikään hänen mittaamansa tulos ei ole yli 39 minuuttia. Ehkä se perustui alustaviin arvioihin?
No, historia osoittaa, että lopullisesti julkaistu tulos on tarkka, joten tuosta ei tarvinne kantaa enempää huolta.
Suomalaisten paikkakuntien pituuspiirit /5/
Pituuspiirin mittaaminen muilla paikkakunnilla oli leveyspiirin mittaamista hankalampaa, koska etukäteen tiedettyjä ja taulukoituja taivaanilmiöitä oli jokapäiväistä auringon kulkua harvemmassa. Jos tuolla hetkellä sää ei ollut suosiollinen, ei Planmanilla ehkä ollut aikaa jäädä odottelemaan parempia kelejä. Siksi hänen onnistui mitata Kajaaninlinnan lisäksi vain viiden paikkakunnan leveyspiirin arvot. Niistäkin Hämeenlinnan lukema leveyspiirin tavoin perustui Rahkoilan mittauksiin.

Rahkoilan mittaus on ainoa, joka on kohtuullisen tarkka. Liperissä suurimman mittausvirheen syy voi olla Planmanin sairastuminen, sillä mittauksen teki apulaispastori Lyra ohjeiden mukaan. Planman toteaakin artikkelissaan: ”Olen kuitenkin aiemmin ilmoittanut sekä seuralaiselleni että apulaispastorille, herra Lyralle, joka oli iloinen voidessaan seurata minua täällä, miten heidän tulisi menetellä Jupiterin kuiden emersioiden tarkkailussa.”
Planmanin havaintopaikat on mainittu sen ajan tapaan selkeästi, mutta pappila, kirkko jne. ovat voineet muuttaa pitemmänkin matkan 260 vuodessa. Näin ei kuitenkaan ole Mikkelin kirkon suhteen, koska tiedetään silloisen puukirkon rakennetun 1750 nykyisen torin paikalle.
Siksi voi olla, että Planman ei ole vieraillut joissakin havaintopaikoissa tarpeeksi kauan varmistaakseen heilurikellonsa tarkkuuden. Silloin mittauksissa on ajanotossa pitänyt olla noin puolentoista minuutin virhe Mikkelissä ja Pielisjärvellä.
Toisaalta leveyspiirin mittaus Mikkelissä on ollut erittäin onnistunut, joten kellon systemaattinen virhe ei tunnu loogiselta. Tällöin virhelähteeksi jää itse ilmiön ajoitus. Kuten yllä olevasta animaatiosta huomataan, Jupiterin kuun katoaminen tapahtuu hetkessä, ja seuraavaa saa odotella sääolosuhteiden armoilla parista päivästä viikkoon.
On myös mahdollista, että Jupiterin kuiden havaintotaulukoissa on ollut heittoa, joskin tiedetään tiedeakatemian sihteeri Pehr Wargentinin jo 1740-luvun alusta lähtien säännöllisesti seuranneen Galilein kuiden kiertoa /6/.
Planmanin tulokset pituuspiirien mittauksissa olivat esitetyn vertailun perusteella suurimmaksi osaksi välttäviä.
Tekoälyn hyödyntäminen tiedonhaussa
Tämä kesäprojektini on ylittänyt orastavat toiveeni selvittää, miten maantieteellinen paikannus tähtitieteen avulla toimi 1760-luvulla. Kiinnostuksen myötä sitä usein huomaa kaivavansa yhä syvempää kuoppaa, mutta itse ainakin huomasin tekoälyn oivaksi työkaluksi.
Sen käyttäminen on selvästi tekniikkalaji, jossa on pyrittävä rajaamaan haut selkeästi ja määrittämään myös niiden laatutaso. Olenkin laittanut sivustollemme osan yhteistyömme alkuajasta, josta selviää erittäin hyvin, miten haastavaa työ on.
Kuitenkin etenin tutkimuksessani huomattavasti pidemmälle sen takia, että eteen tuli tekoälyn kautta myös selkeää tietoa, jota tuskin olisin muuten kohdannut. Ja tietohan kasvaa portaittain.
Tekoälyn käyttöjärjestelmässä on pitemmän päälle ärsyttäviä piirteitä. Sen lattiaan saakka kumartava tapa pyytää virheitään anteeksi ensiksi naurattaa, mutta kun asiaa ei siltikään saa etenemään, virnistykset kyllä tukahtuvat. Toinen ärsyttävä piirre on se yletön mairittelevuus etenkin käyttäjän ajatusten ja hänen itsesä löytämien tietojen kommentoinnissa. En myöskään tahdo aina löytää oikeaa tapaa estää olemattomien tietojen keksimistä, jotka voivat helposti hukkua faktan keskelle. Ja vaikka pyytää tekoälyä sanomaan, ettei se tiedä, ei siitä tule mitään. Kas kun se ei tiedä ettei se tiedä.
Mutta kokemuksia tasapainottavia positiivisia puolia on saada tiedonmurusia sieltä täältä hieman irrallaan oleviin asioihin, joista on hyvä lähteä kuromaan tietoja yhteen. Ja tässä tapauksessa asiat lähtivät rullaamaan toden teolla tekoälyn käännettyä latinankielisen artikkelin.
Tosin meni aikaa ymmärtää, ettei tekoäly pysty avaamaan ja lukemaan linkkejä, vaan se vastaa oikein, jos asianomaista tekstiä on käytetty oppimisessa. Sen vuoksi tekoälyn suosittelemat lähteet eivät yleensä toimi. Siitä on hyvänä esimerkkinä linkittämäni ’muistelman’ alkuvaihe, jossa kulmakarvat vähintään nousivat, kun linkit eivät johtaneet mihinkään.
Koska tekoäly löysi kohtia kaikista käytetyistä lähteistä, olivat nuo yli 250 vuotta vanhat julkaisut olleet myös sen virittämisessä mukana.
Tekoäly osaa myös suomea hyvin, ja tekstintarkistajana kyllä löytää hyvin ajatus- ja kirjoitusvirheet.
Ja kaikkein tärkeintä on, että tarkistaa kaiken, mitä yhteistyön perusteella saa selville.
[1] Planman, Anders. Expositio observationum transitus Veneris per solem, Cajaneburgi a:o 1769 D. 3 Junii factarum, Carl Widqvistin maisteripresentaatio, Turun Akatemia 1770. (1700-luvulla maisterintutkintoon kuului esittää professorin kirjoittama väitöskirja)
[2] Planman, Anders. DISSERTATIO DE VENERE IN SOLE VISA DIE 6 JUNII ANNI 1761,Anders Planmanin väitöskirja 23.2.1763, Turun Akatemia, 1763.
[2] Planman, Anders. Cajaneborgs geografiska belägenhet, Kungliga Svenska Vetenskapsakademiens Handlingar, April, Maj och Juni i år 1762, pp. 132 – 139.
[3] Pekonen, Osmo. The Amateur Astronomer Anders Hellant and the Plight
of his Observations of the Transits of Venus in Tornio, 1761 and 1769. Journal of Astronomical Data, 2013.
[4] Wargentin, Pehr. OBSERVATIONER På Planeten Veneris gång genom Solens Discus, om äro gjorde i Stockholm, Upsala, Åbo, Carlscrona, Lund, Landscrona, Cajaneborg den 6 Junii 1761. Kungliga Svenska Vetenskapsakademiens Handlingar, April, Maj och Juni i år 1761, pp. 143 – 166.
[5] Planman, Anders. Astronomiska observationer under resan til och ifrån Cajaneborg, gjorde år 1761. Kungliga Svenska Vetenskapsakademiens Handlingar, Januari, Februari och Mars i år 1767, pp. 132 – 139.
[6] Kärnfelt, Johan. ‘Excellentissimo tubo Dollondiana’: The Stockholm Observatory’s 10-foot Dollond achromatic refractor, Journal of the History of Astronomy. Vol 5, Issue 1.
